堆
堆数据结构的特性
数组表示(节点x;左子节点2x;右子节点2x+1)
完全二叉树、最后一层左子树开始填写
最大堆、最小堆定义:除了根节点最大或者最小,其他子节点不会大过(不会小于)父节点的值
利用最小堆、最大堆得性质,逐步移除根节点,那么结果则为已排序数据。
举例数据:
1 | {4,1,3,2,16,9,10,14,8,7} |
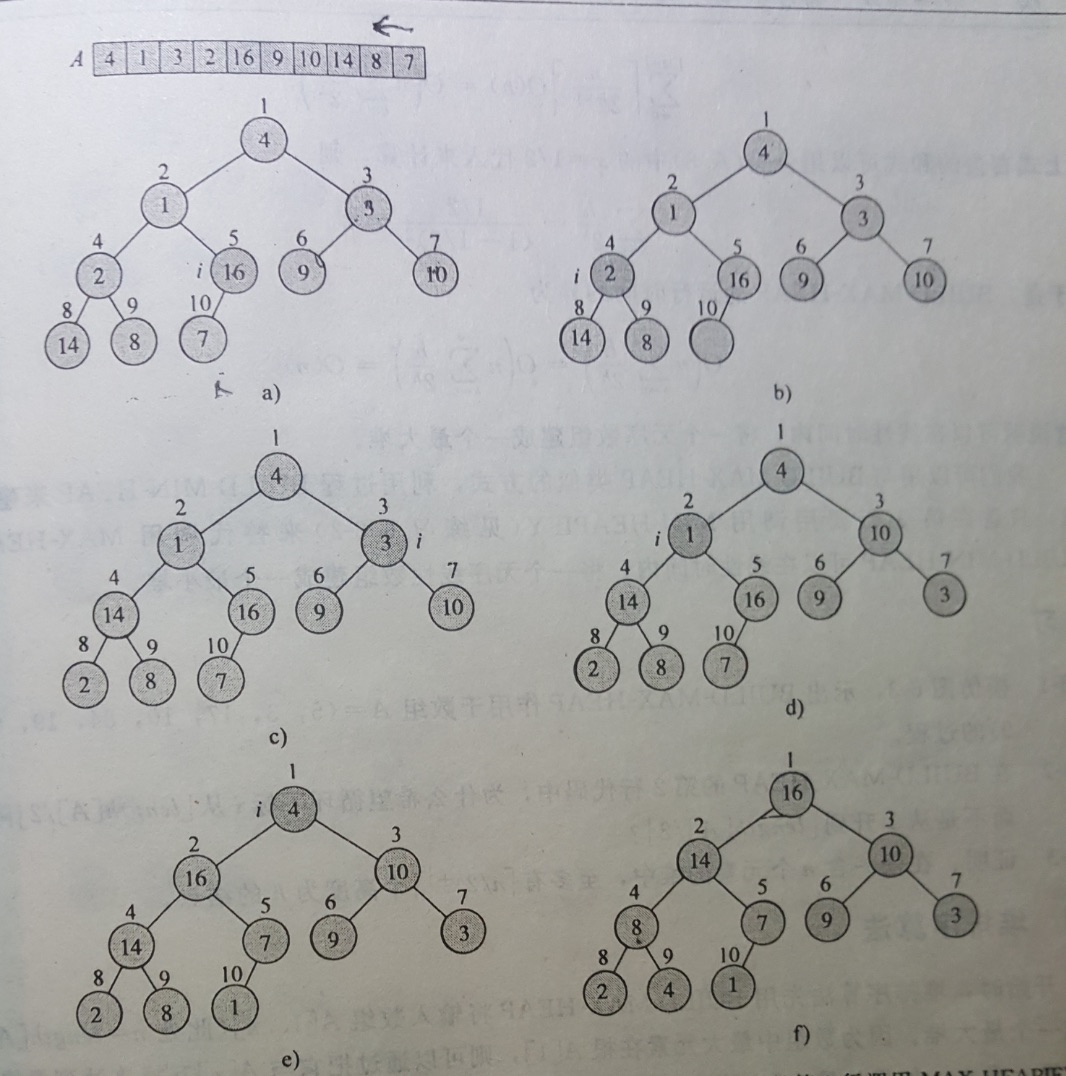
构建堆(大根堆)
堆排序分为如下几个步骤 a~f
- a) 数据数据堆表示
- b) 自底向上,数据7的父元素i(i–)维持最大堆特性
- c)~e) 按照对特性,循环保持
- f) 完成后的最大堆
堆排序
- 构建最大堆(对应升序排列)
- 从堆长度位置(数组尾部)开始遍历
- 交换A[i]与A[1]; 堆长度减一,因为交换前A1为最大元素
- 调整堆保持最大堆特性:adjust(A,1)。每次调整的代价为O(lg(n))
- i=2 退出循环,得到升序数组。 那么时间复杂度为n*O(lg(n))
上述流程的过程图如下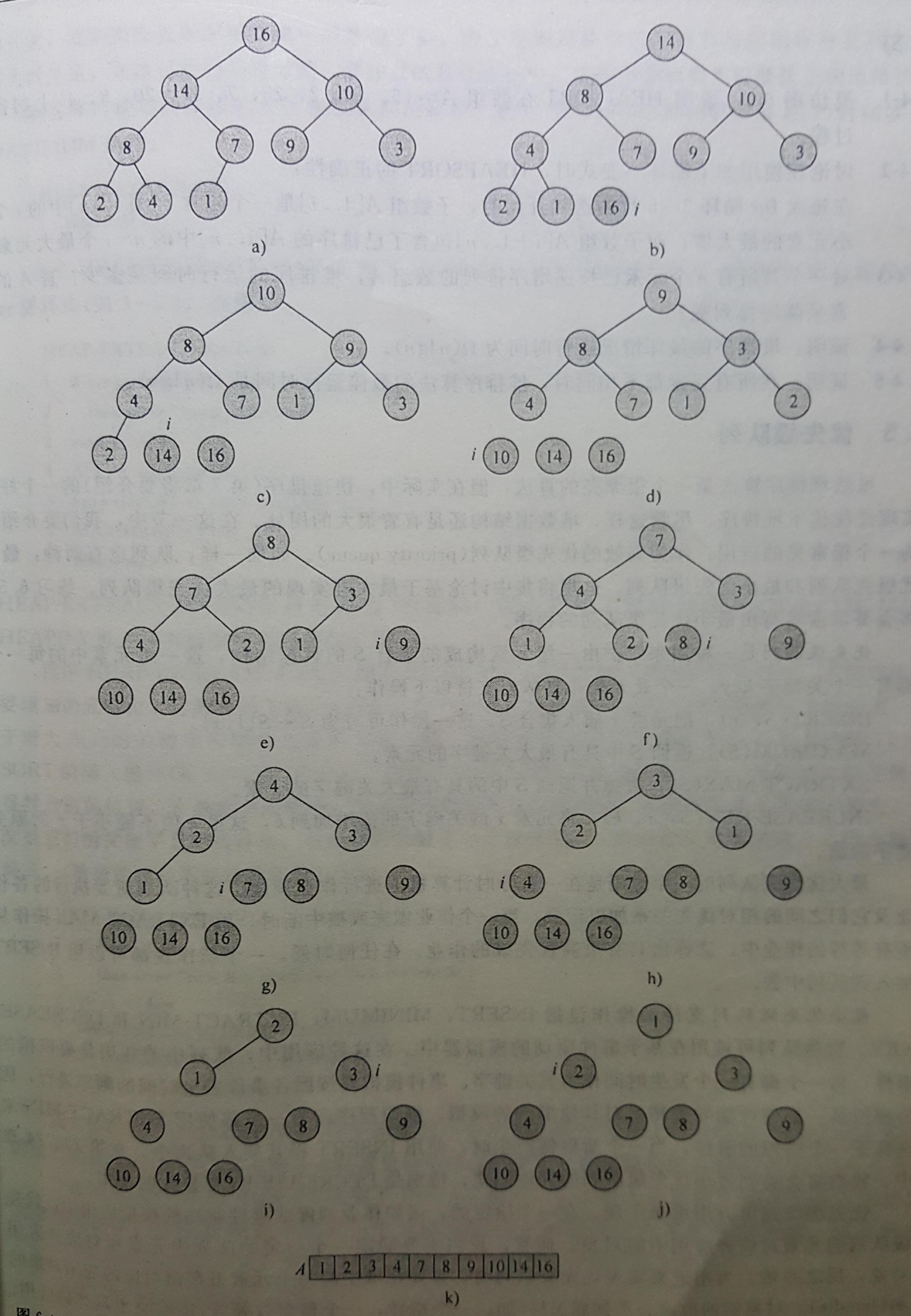
总结
- 初始化堆,即构建
- 维持堆特性,主要包含上浮、下沉操作
版权声明:本文为博主原创文章,未经允许不得转载。